时间限制:1000ms
单点时限:1000ms
内存限制:64MB
描述
小Hi和小Ho是一对好朋友,出生在信息化社会的他们对编程产生了莫大的兴趣,他们约定好互相帮助,在编程的学习道路上一同前进。
这一天,他们遇到了一连串的字符串,于是小Hi就向小Ho提出了那个经典的问题:“小Ho,你能不能分别在这些字符串中找到它们每一个的最长回文子串呢?”
小Ho奇怪的问道:“什么叫做最长回文子串呢?”
小Hi回答道:“一个字符串中连续的一段就是这个字符串的子串,而回文串指的是12421这种从前往后读和从后往前读一模一样的字符串,所以最长回文子串的意思就是这个字符串中最长的身为回文串的子串啦~”
小Ho道:“原来如此!那么我该怎么得到这些字符串呢?我又应该怎么告诉你我所计算出的最长回文子串呢?
小Hi笑着说道:“这个很容易啦,你只需要写一个程序,先从标准输入读取一个整数N(N<=30),代表我给你的字符串的个数,然后接下来的就是我要给你的那N个字符串(字符串长度<=10^6)啦。而你要告诉我你的答案的话,只要将你计算出的最长回文子串的长度按照我给你的顺序依次输出到标准输出就可以了!你看这就是一个例子。”
- 样例输入
-
3abababaaaaabaaacacdas
样例输出 -
753
传说中的Manacher算法,算法的核心就在这一句上了:p[i] = min(p[2*id-i], p[id] + id - i);
原文地址:
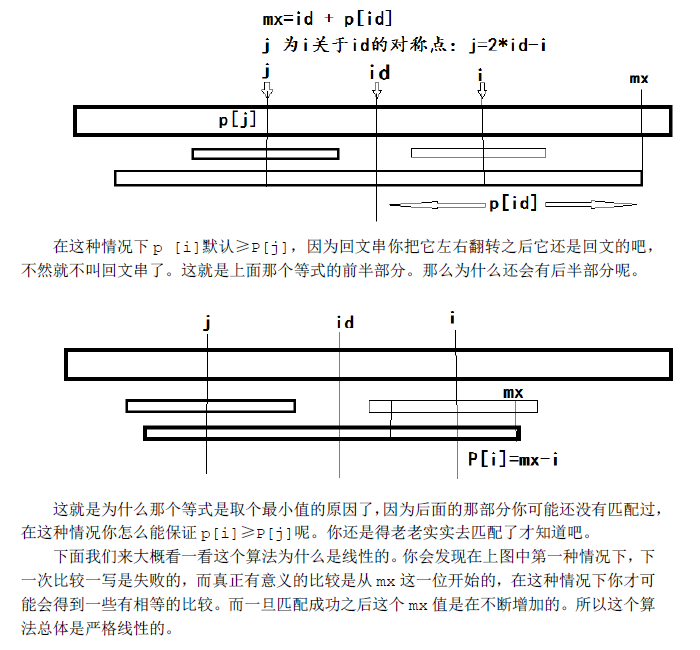
其实原文说得是比较清楚的,只是英文的,我这里写一份中文的吧。 首先:大家都知道什么叫回文串吧,这个算法要解决的就是一个字符串中最长的回文子串有多长。这个算法可以在O(n)的时间复杂度内既线性时间复杂度的情况下,求出以每个字符为中心的最长回文有多长, 这个算法有一个很巧妙的地方,它把奇数的回文串和偶数的回文串统一起来考虑了。这一点一直是在做回文串问题中时比较烦的地方。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性,避免了大量不必要的重复匹配。 算法大致过程是这样。先在每两个相邻字符中间插入一个分隔符,当然这个分隔符要在原串中没有出现过。一般可以用‘#’分隔。这样就非常巧妙的将奇数长度回文串与偶数长度回文串统一起来考虑了(见下面的一个例子,回文串长度全为奇数了),然后用一个辅助数组P记录以每个字符为中心的最长回文串的信息。P[id]记录的是以字符str[id]为中心的最长回文串,当以str[id]为第一个字符,这个最长回文串向右延伸了P[id]个字符。 原串: w aa bwsw f d 新串: # w# a # a # b# w # s # w # f # d #辅助数组P: 1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1 这里有一个很好的性质,P[id]-1就是该回文子串在原串中的长度(包括‘#’)。如果这里不是特别清楚,可以自己拿出纸来画一画,自己体会体会。当然这里可能每个人写法不尽相同,不过我想大致思路应该是一样的吧。 好,我们继续。现在的关键问题就在于怎么在O(n)时间复杂度内求出P数组了。只要把这个P数组求出来,最长回文子串就可以直接扫一遍得出来了。 由于这个算法是线性从前往后扫的。那么当我们准备求P[i]的时候,i以前的P[j]我们是已经得到了的。我们用mx记在i之前的回文串中,延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。(注:为了防止字符比较的时候越界,我在这个加了‘#’的字符串之前还加了另一个特殊字符‘$’,故我的新串下标是从1开始的) if( mx > i)
p[i]= MIN( p[2*id-i], mx-i);
就是当前面比较的最远长度mx>i的时候,P[i]有一个最小值。这个算法的核心思想就在这里,为什么P数组满足这样一个性质呢?
(下面的部分为图片形式)
1 #include2 using namespace std; 3 4 int N; 5 string s; 6 7 void solve() { 8 string s1; 9 s1.resize(2 * s.size() + 2);10 s1[0] = '$';11 s1[1] = '#';12 for (int i = 0; i < s.size(); ++i) {13 s1[(i + 1) << 1] = s[i];14 s1[((i + 1) << 1) + 1] = '#';15 }16 vector p(s1.size(), 0);17 int res = 0;18 for (int id = 0, i = 1; i < s1.size(); ++i) {19 if (p[id] + id > i) p[i] = min(p[2 * id - i], p[id] + id - i);20 else p[i] = 1;21 while (s1[i + p[i]] == s1[i - p[i]]) ++p[i];22 if (i + p[i] > id + p[id]) id = i;23 res = max(res, p[i]);24 }25 cout << res - 1 << endl;26 }27 28 int main() {29 cin >> N;30 while (N--) {31 cin >> s;32 solve();33 }34 return 0;35 }